Facebook Hacker Cup 2021 Qualification Round
Facebook Hacker Cup est un concours de programmation international annuel hébergé et administré par Facebook.
Demain va se tenir le round 1 du concours. Pour participer à ce round, il faut avoir résolu au moins un exercice sur 5 lors du round de Qualification. Dans cet article, je vous présente les solutions des trois problèmes que j’ai résolu.
Bien que je présenterai, les énnoncés de chaque problème, je vous invite à aller les voir vous-même ici et par la même occasion essayer vos solutions.
Problem 1 : Consistency Chapitre 1 (11 pts)
Le problème est le suivant: Connie a reçu une chaîne S pour son anniversaire, composée entièrement de lettres majuscules (chacune entre “A” et “Z”, inclus).
Cependant, Connie n’aime vraiment que les chaînes agréables et cohérentes. Elle considère qu’une chaîne est cohérente si et seulement si toutes ses lettres sont identiques.
Chaque seconde, Connie peut choisir une lettre dans S et la remplacer par une lettre différente. Si la lettre qu’elle a choisie est une voyelle, elle peut la remplacer par n’importe quelle consonne de son choix. D’un autre côté, si la lettre qu’elle a choisie est une consonne, alors elle peut la remplacer par n’importe quelle voyelle de son choix. Les 5 lettres “A”, “E”, “I”, “O” et “U” sont considérées comme des voyelles, tandis que les 21 lettres restantes de l’alphabet sont considérées comme des consonnes. Si une lettre apparaît plusieurs fois dans S, elle ne peut remplacer qu’une seule occurrence par seconde.
Aidez-la à déterminer le nombre minimum de secondes nécessaires pour transformer S en n’importe quelle chaîne cohérente. Notez que S peut déjà être cohérent, auquel cas 0 seconde serait nécessaire.
Réflexion
Résolvons d’abord quelques exemples à la main.
Exemple 1
S = ABC
Connie pourrait remplacer les deuxième et troisième lettres (“B” et “C”) chacune par “A”, produisant la chaîne “AAA” en 2 secondes.
Example 2
S = F
“F” est déjà cohérent. Le résultat est donc 0 seconde.
Example 3
S = BANANA
Connie pourrait remplacer les première, troisième et cinquième lettres (“B”, “N” et “N”) chacune par “A”, produisant la chaîne “AAAAAA” en 3 secondes.
Pour résoudre ce problème, nous pouvons implémenter un algorithme de brute force qui consistera à calculer le temps minimum qu’il faut pour transformer la chaîne S en une chaîne consistante pour toutes les lettres de l’alphabet. Le minimum de tous ces temps sera notre résultat.
Soient Ai la ième lettre de l’alphabet, Ti le temps qu’il faut pour transformer S en une chaîne consistante ayant pour lettre Ai.
-
On initialise Ti à 0.
-
Pour chaque lettre Ls de S:
-
Si Ls == Ai: Ti reste inchangé
-
Si Ls et Ai sont toutes les deux des voyelles ou des consonnes: On ajoute 2 à Ti (puisqu’il faut d’abord changer Ls en voyelle ou en consonne selon le cas avant de la transformer en Ai)
-
Sinon: On ajoute 1 à Ti
-
Notre résultat est le minimum de tous les Ti
SOLUTION PYTHON 3:
import sys
import string
from collections import Counter
sys.stdin = open("consistency_chapter_1_input.txt")
sys.stdout = open("ans_a1.txt", "w")
vowels = 'AEIOU'
alphabet = string.ascii_uppercase
def are_same(a, b):
return (a in vowels and b in vowels) or (not a in vowels and not b in vowels)
def solve():
s = list(input())
ans = float('inf')
for target in alphabet:
target_ans = 0
for l in s:
if l == target:
continue
if are_same(target, l):
target_ans += 2
else:
target_ans += 1
ans = min(ans, target_ans)
return ans
for t in range(int(input())):
print('Case #{}: {}'.format(t+1,solve()))
Problem 2 : Consistency Chapitre 2 (17 pts)
Le problème est le suivant: Connie a reçu une chaîne S pour son anniversaire, composée entièrement de lettres majuscules (chacune entre “A” et “Z”, inclus).
Cependant, Connie n’aime vraiment que les cordes agréables et cohérentes. Elle considère qu’une chaîne est cohérente si et seulement si toutes ses lettres sont identiques.
Chaque seconde, Connie peut choisir une lettre dans S et la remplacer par une lettre différente. Il existe K types de remplacements différents qu’elle peut effectuer, le ième impliquant le choix de la lettre Ai n’importe où dans S et en le remplaçant par la lettre Bi. Aucun type de remplacement (Ai, i) n’est donné deux fois.
Il n’y a aucune limite sur le nombre de fois qu’elle peut finir par utiliser chaque type de remplacement. Si une lettre apparaît plusieurs fois dans S, elle ne peut remplacer qu’une seule occurrence par seconde.
Aidez-la à déterminer le nombre minimum de secondes nécessaires pour transformer S en n’importe quelle chaîne cohérente, si possible. S’il est impossible de le faire, affichez -1 à la place. Notez que SS peut déjà être cohérent, auquel cas 0 seconde serait nécessaire.
Réflexion
Ce problème est une variante du problème 1. La différence se trouve dans le fait que l’on a K couples (Ai, Bi) et pour chaque occurence Ai de S, il est possible de la remplacer par Bi
Exemple 1
S = ABC
K = 2
Remplacement 1: BA
Remplacement 2: CA
Connie pourrait remplacer les deuxième et troisième lettres (“B” et “C”) chacune par “A”, produisant la chaîne “AAA” en 2 secondes en utilisant respectivement le remplacement 1 pour “B” et le remplacement 2 pour “C”.
Example 2
S = FOXEN
K = 8
Remplacement 1: NI
Remplacement 2: OE
Remplacement 3: NX
Remplacement 4: EW
Remplacement 5: OI
Remplacement 6: FE
Remplacement 7: FN
Remplacement 8: XW
Pour résoudre ce problème, nous pouvons construire un graphe orienté G = (V, E):
-
V l’ensemble des sommets (Toutes les lettres de l’alphabet dans notre cas)
-
E → {(x, y) (x, y) ∈ V2 ∧ x ≠ y}
Dans notre cas E est l’ensemble des K couples (Ai, Bi)
Voici ci dessous le graphe représentant l’exemple 2:
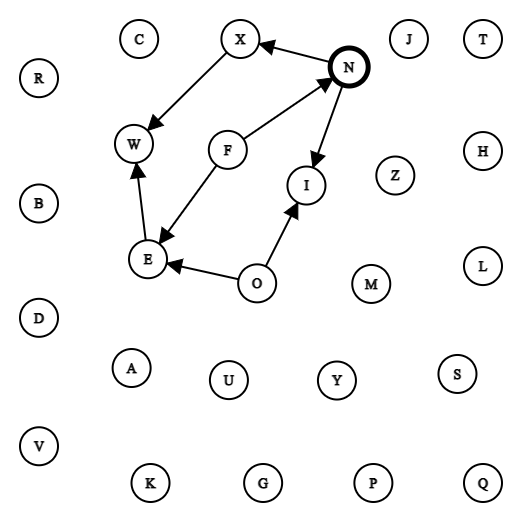
Vous vous demandez sûrement comment nous allons pouvoir trouver la solution avec cela. Ne vous inquitez pas, nous y sommes. Tout d’abord considérez chaque sommet du graphe comme une ville et chaque ligne orientée comme un chemin.
Soit Tv la somme des distances minimales qu’il faut pour atteindre la ville v à partir des autres villes.
Notre résultat est le minimum de tous les Tv.
Nous utiliserons une variante de l’algorithme de Dijkstra: le BFS qui permettra de calculer les distances de toutes les villes depuis une ville source en considérant que la valeur d’un chemin est 1 (1 seconde dans notre cas).
SOLUTION C++:
#include <bits/stdc++.h>
using namespace std;
using str=string;
const int64_t MOD=1000*1000*1000+7;
const str alphabet="abcdefghijklmnopqrstuvwxyz";
const double pi = std::acos(-1);
#define pii pair<int64_t,int64_t>
#define psi pair<str, int64_t>
#define pis pair<int64_t, str>
#define msi map<str, int64_t>
#define mis map<int64_t, str>
#define vec vector
#define ll long long
#define ull unsigned long long
#define for_n(i,n) for(int64_t i=0; i<n; ++i)
#define pb(x) push_back(x)
#define ins(x) insert(x)
#define all(x) x.begin(),x.end()
#define be begin()
#define en end()
#define rbe rbegin()
#define ren rend()
#define findIn(x,y) find(all(x),y)
#define mk make_pair
const int64_t oo = 1000*1000*1000;
map<char, int64_t> dists;
map<char, set<char>> noeuds;
void BFS (const char start)
{
for(char c = 'A'; c <= 'Z'; c++)
{
dists[c] = +oo;
}
queue< pair<char, int64_t> > aVoir; // {iNoeud, dist}
aVoir.push( make_pair(start, 0) );
while (aVoir.size()) {
const char iNoeud = aVoir.front().first;
const int64_t dist = aVoir.front().second;
aVoir.pop();
if (dists[iNoeud]<oo) {
continue;
}
dists[iNoeud] = dist;
for (const char voisin : noeuds[iNoeud]) {
aVoir.push( make_pair(voisin, dist+1) );
}
}
}
int64_t solve()
{
string s;
cin>>s;
char a=s[0];
bool ok =true;
for(auto c: s)
{
if(c!=a){
ok = false;
break;
}
}
int64_t k;
cin>>k;
noeuds.clear();
while(k--)
{
string x;
cin>>x;
noeuds[x[0]].insert(x[1]);
}
if(ok) return 0;
if(noeuds.size()==0) return -1;
int64_t ans = oo;
map<char, int64_t> allDists;
for(auto x: s)
{
BFS(x);
for(auto p: dists){
allDists[p.first] += p.second;
}
}
for(auto p: allDists){
if(p.second>=0)
ans = min(ans, p.second);
}
if(ans<oo)
{
return ans;
}
else{
return -1;
}
}
int main ()
{
ios_base::sync_with_stdio(false); cin.tie(NULL);
freopen("test.txt", "r",stdin);
freopen("ans2.txt", "w", stdout);
int64_t t;
cin >> t;
for(int64_t i=1; i<=t; i++)
{
printf("Case #%lld: %lld\n", i, solve());
}
}
Problem 3 : Xs and Os (15 pts)
Le problème est le suivant: Vous jouez contre un adversaire sur une grille de cellules avec N lignes et N colonnes. Toutes les cellules sont initialement vides, et les deux joueurs placent normalement à tour de rôle des symboles dans des cellules vides (avec un joueur plaçant Xs et l’autre plaçant Os) jusqu’à ce qu’une ligne et/ou une colonne soit entièrement remplie avec les symboles d’un joueur (en ce moment le jeu se termine avec ce joueur gagnant) ou toutes les cellules ont été remplies sans qu’aucun des deux joueurs ne gagne (auquel cas le jeu se termine par un match nul). Notez qu’un joueur remplissant une diagonale entière avec ses symboles ne le fait pas gagner.
Ce jeu particulier est en train d’être joué, avec vous plaçant Xs et votre adversaire plaçant Os. L’état actuel de la cellule dans la ième ligne à partir de la colonne supérieure et la jième colonne à partir de la gauche est l’un des suivants :
-
si Cij = “.”, la cellule est toujours vide
-
si Cij = “X”, un X a été placé dans la cellule
-
sinon, si Cij = “O”, un O a été placé dans la cellule
Dans l’état actuel du jeu, les deux joueurs ont effectué un nombre égal de tours (en d’autres termes, le nombre de X est le même que le nombre d’O), aucun des deux joueurs n’a encore gagné et le jeu ne s’est pas encore terminé par un match nul. (ce qui signifie qu’au moins une cellule est encore vide).
Votre adversaire vient de tourner le dos, vous donnant la possibilité de placer immédiatement autant de X supplémentaires que vous le souhaitez sur le plateau, dans n’importe quel ensemble de cellules vides. Déterminez le nombre minimum de X supplémentaires que vous devez placer de manière à ce que les placer vous fasse gagner immédiatement (en raison d’une ligne et/ou d’une colonne entièrement remplie de X), si cela est possible. Si cela est possible, vous devez également déterminer le nombre d’ensembles différents de cellules dans lesquels ce nombre minimum de X pourrait être placé. Deux ensembles de cellules sont considérés comme différents si l’un d’eux comprend au moins une cellule que l’autre n’a pas.
Réflexion
Exemple 1
N = 2
XO
..
Il y a une façon de placer seulement 1 X supplémentaire et de gagner. Vous pouvez le placer dans le coin inférieur gauche (remplissant ainsi toute la colonne de gauche) :
XO
X.
Example 2
N = 3
…
…
…
Vous devrez placer 3 X pour gagner, et vous pouvez choisir l’un des 6 ensembles de cellules suivants pour les placer :
XXX … … X.. .X. ..X
… XXX … X.. .X. ..X
… … XXX X.. .X. ..X
La résolution de ce problème consiste à parcourir toutes les lignes et colonnes de la grille. Pour une ligne ou une colonne donnée, si elle n’a pas d’Os et a k espaces vides, alors vous pouvez gagner en y plaçant k X (en remplissant les espaces vides). La première partie de la réponse est donc la valeur minimale de k sur toutes ces lignes et colonnes, et il est impossible de gagner s’il n’y en a pas.
S’il est possible de gagner, alors la deuxième partie de la réponse est égale au nombre d’ensembles distincts de cellules vides (dans lesquelles les X seront placés) dans ces lignes/colonnes à k minimum.
SOLUTION PYTHON 3:
import sys
import string
from collections import Counter
sys.stdin = open("xs_and_os_validation_input.txt")
sys.stdout = open("ans_b.txt", "w")
def solve():
N = int(input())
grid = ['']*N
ans = float('inf')
set_of_cell = list()
for i in range(N):
l = input()
x = l.count('X')
if not 'O' in l:
if N - x < ans:
ans = N - x
set_of_cell = list()
w = ' '.join(str(i)+str(j) for j in range(N) if l[j]=='.')
set_of_cell.append(w)
elif N - x == ans:
w = ' '.join((str(i)+str(j) for j in range(N) if l[j]=='.'))
if not w in set_of_cell:
set_of_cell.append(w)
for j in range(N):
grid[j] += l[j]
i = 0
for l in grid:
x = l.count('X')
if not 'O' in l:
if N - x < ans:
ans = N - x
set_of_cell = list()
w = ' '.join(str(j)+str(i) for j in range(N) if l[j]=='.')
set_of_cell.append(w)
elif N - x == ans:
w = ' '.join(str(j)+str(i) for j in range(N) if l[j]=='.')
if not w in set_of_cell:
set_of_cell.append(w)
i+=1
if ans < float('inf'):
print(ans, len(set_of_cell))
else:
print('Impossible')
for t in range(int(input())):
print('Case #{}:'.format(t+1), end=' ')
solve()
Voilà nous sommes à la fin de cet article, j’espère qu’il vous aura plus. N’hésitez pas à le partager et à me suivre sur facebook et twitter pour être au courant de mes prochaines publications.
